Méthode de newton
Description de la méthode
Soit $f$ une fonction réelle.
On cherche la solution $\alpha$ de l’équation $f(x) = 0$
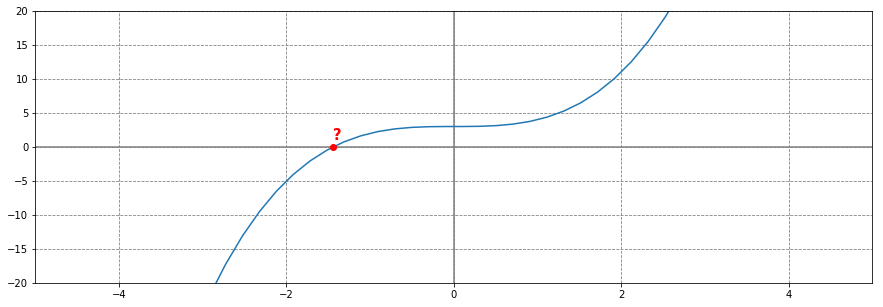
On part d’une valeur $x_0$ au hasard (sous certaines conditions) et on trace la tangente $T_1$ à la courbe $\mathcal{C}_f$ de $f$ en $x_0$
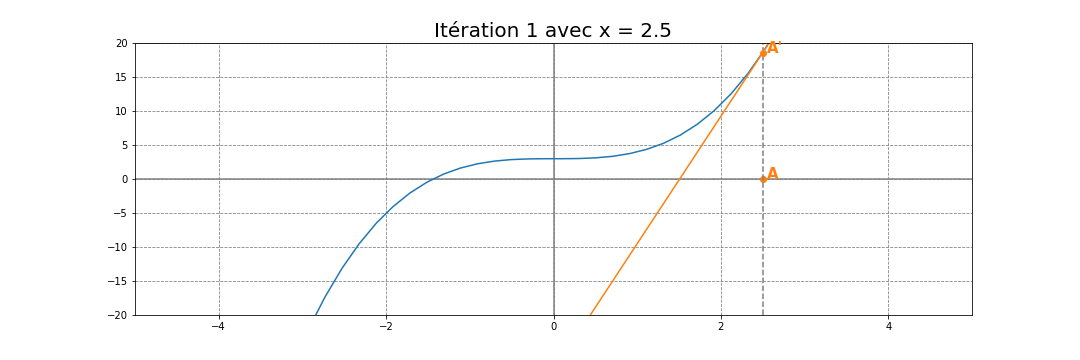
L’abscisse $x_1$ du point d’intersection de la tangente $T_1$ avec l’axe des abscisses est une valeur approchée de la solution $\alpha$
Quelle est la formule de $x_1$ en fonction de $x_0$ ?
On réitère ce même principe un certain nombre
de fois avec $x_n$ et la tangente $T_n$ au point d’abscisse $x_{n-1}$.
On obtient donc une suite $\left ( x_n \right )_{n}$ qui converge vers
la solution $\alpha$
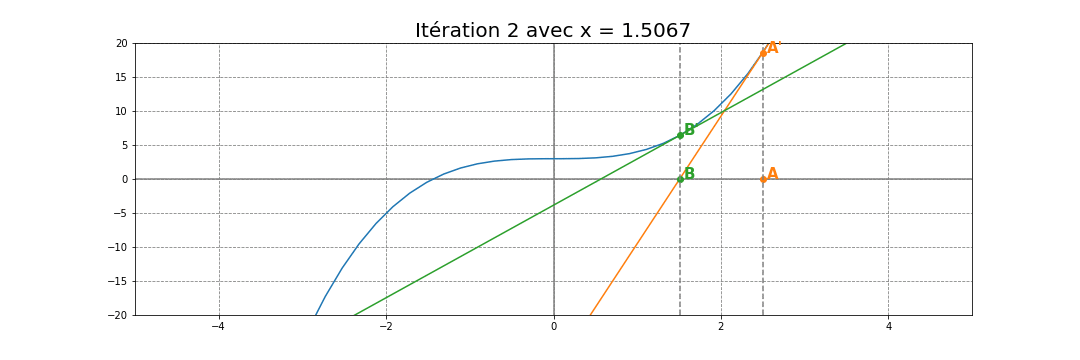
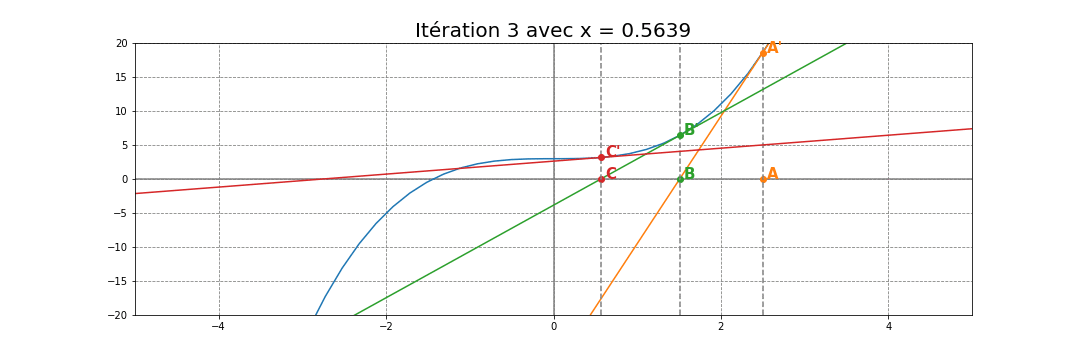
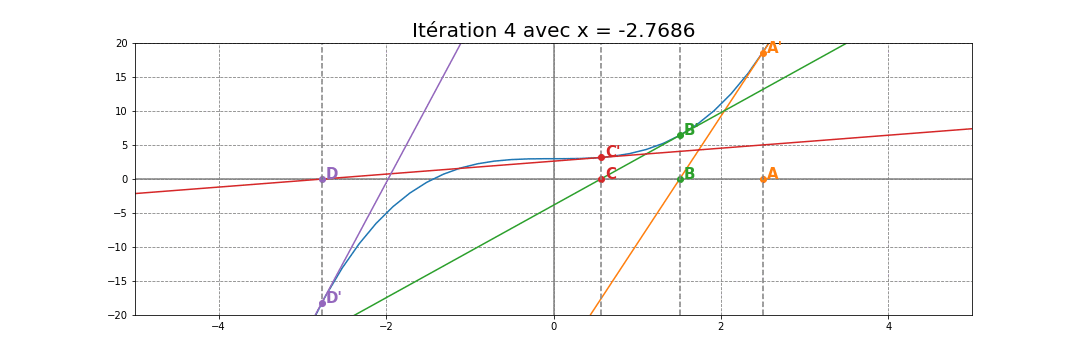
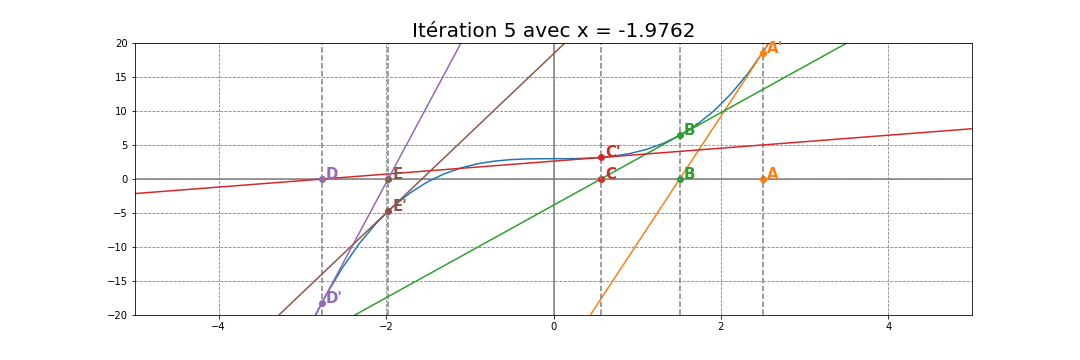
La suite $\left ( x_n \right )_{n}$ est donc définie par la relation de récurrence :
A retenir $$x_n = x_{n-1} - \frac{f(x_{n-1})}{{f}’(x_{n-1})}$$
Mise en œuvre pratique
Une première implémentation :
def newton(f, df, x0, eps=2**-50):
x = x0
while ( abs(f(x)) > eps ):
x = x - f(x) / df(x)
return xAjout du paramètre max_iter :
def newton(f, df, x, eps=2**-50, max_iter = 100):
i = 0
while ( abs(f(x)) > eps and i < max_iter):
x = x - f(x) / df(x)
i = i + 1
return xApplications
On souhaite calculer une valeur approchée de $\sqrt{2}$.
On construit donc la fonction $f(x) = x^2 - 2$ qui a pour racines
$\sqrt{2}$ et $-\sqrt{2}$
La racine obtenue dépendra du choix de $x_0$
def newton(f, df, x, eps=2**-50, max_iter = 100):
i = 0
while ( abs(f(x)) > eps and i < max_iter):
x = x - f(x) / df(x)
i = i + 1
return x
def f(x):
return x**2 - 2
def df(x):
return 2*x
print(newton(f, df, 1))On peut également utiliser la fonction newton du package scipy.optimize
from scipy.optimize import newton
def f(x):
return x**2 - 2
def df(x):
return 2*x
print(newton(f, 1, df))Avantages et inconvénients de la méthode de Newton
Avantages
Convergence quadratique : La méthode de Newton converge beaucoup plus rapidement que d’autres méthodes (comme la dichotomie) lorsque le point initial est suffisamment proche de la solution. Le nombre de décimales exactes double approximativement à chaque itération.
Précision élevée : Elle permet d’obtenir des approximations très précises en peu d’itérations.
Généralisation possible : La méthode peut être étendue aux systèmes d’équations non linéaires et aux équations dans des espaces de dimension supérieure.
Applications diverses : Utile dans de nombreux domaines comme l’optimisation numérique, la résolution d’équations différentielles, le calcul d’inverses et de racines.
Utilisable pour d’autres calculs : La méthode peut être adaptée pour calculer efficacement des inverses de matrices, des racines carrées, cubiques ou d’ordre n.
Inconvénients
Nécessite la dérivée : La méthode exige que la fonction soit dérivable et que sa dérivée soit calculable, ce qui n’est pas toujours possible ou simple.
Sensibilité au point de départ : Le choix du point initial est crucial. Un mauvais choix peut conduire à une divergence ou à la convergence vers une solution non désirée.
Problèmes aux points critiques : La méthode échoue si la dérivée s’annule ou devient très petite près de la solution (ce qui peut causer des divisions par des valeurs proches de zéro).
Convergence non garantie : Contrairement à la dichotomie, la méthode de Newton ne garantit pas toujours la convergence.
Comportement chaotique possible : Pour certaines fonctions, la suite des approximations peut avoir un comportement erratique ou chaotique.
Coût de calcul par itération : Chaque itération nécessite le calcul de la fonction et de sa dérivée, ce qui peut être coûteux pour des fonctions complexes.
Amélioration de la méthode de Newton
Pour pallier certains inconvénients, des variantes de la méthode de Newton ont été développées :
- Méthode de Newton amortie : Introduit un facteur d’amortissement pour améliorer la convergence dans les cas difficiles.
- Méthode de Newton-Raphson modifiée : Évite de recalculer la dérivée à chaque étape pour des fonctions coûteuses.
- Méthode de Newton avec globalisation : Combine la méthode de Newton avec d’autres techniques pour garantir la convergence.
Comparaison avec la méthode de Newton
| Méthode | Convergence | Conditions | Avantages | Inconvénients |
|---|---|---|---|---|
| Dichotomie | Linéaire | $f$ continue, $f(a) \times f(b) < 0$ | Simple, robuste | Lente |
| Newton | Quadratique | $f$ dérivable, $f’$ non nulle près de la solution, bon point de départ | Rapide | Peut diverger, nécessite la dérivée |
La méthode de Newton converge plus rapidement que la dichotomie lorsque les conditions sont favorables, mais la dichotomie est plus robuste et garantit la convergence dans tous les cas où les conditions initiales sont respectées.